Distance Metrics in Machine Learning

Correlation measures only linear codependence, which can be misleading. Also, it does not satisfy properties of a metric, like nonnegativity and triangle inequality. A metric $d_{\rho}[X, Y]=\sqrt{1 / 2(1-\rho[X, Y])}$ can be formed using correlation. This metric essentially inherits properties from Euclidean distance after z-standardization, making it a 'true metric'.

Another normalized correlation-based distance metric, $d_{|\rho|}[X, Y]=\sqrt{1-|\rho[X, Y]|}$, can also be defined. This metric is especially useful when you need to consider negative correlations as similar for particular applications.

def calculate_distance(
    dependence: np.ndarray,
    metric: str = "angular"
) -> np.ndarray:
    if metric == "angular":
        distance = ((1 - dependence).round(5) / 2.) ** 0.5
    elif metric == "absolute_angular":
        distance = ((1 - abs(dependence)).round(5) / 2.) ** 0.5
    return distance

Information Theory: Marginal and Joint Entropy

Correlation has limitations: it neglects nonlinear relationships, is sensitive to outliers, and is mostly meaningful for normally-distributed variables. To address this, we can use Shannon's entropy, defined for a discrete random variable $X$:

This entropy $H[X]$ measures the amount of uncertainty or 'surprise' associated with $X$.

For two discrete random variables $X, Y$, the joint entropy is:

Conditional Entropy

Conditional entropy $H[X|Y]$ measures the remaining uncertainty in $X$ when $Y$ is known:

Divergence Measures: Kullback-Leibler and Cross-Entropy

Kullback-Leibler (KL) divergence quantifies how one probability distribution $p$ diverges from another $q$:

Cross-entropy $H_C[p \| q]$ measures the information content using a wrong distribution $q$ rather than the true distribution $p$:

import numpy as np

def calculate_kullback_leibler_divergence(
    p: np.ndarray,
    q: np.ndarray
) -> float:
    divergence = -(p * np.log(q / p)).sum()
    return divergence


def calculate_cross_entropy(
    p: np.ndarray,
    q: np.ndarray
) -> float:
    entropy = -(p * np.log(q)).sum()
    return entropy

Mutual Information

The mutual information $I[X;Y]$ measures the amount of information $X$ and $Y$ share:

It can be further generalized to a metric form using normalized mutual information $NMI$ to fulfill metric properties.

Conclusion

Both correlation and entropy-based measures have their places in modern applications. Correlation-based measures are computationally less demanding and have a long history in statistics. In contrast, entropy-based measures provide a comprehensive understanding of relationships between variables. Implementing these concepts can enhance your analytics and decision-making processes.

import numpy as np
from sklearn.metrics import mutual_info_score
import scipy.stats as ss

def calculate_number_of_bins(
    num_observations: int,
    correlation: float = None
) -> int:
    if correlation is None:
        z = (8 + 324 * num_observations + 12 * (36 * num_observations + 729 * num_observations ** 2) ** .5) ** (1 / 3.)
        bins = round(z / 6. + 2. / (3 * z) + 1. / 3)
    else:
        bins = round(2 ** -.5 * (1 + (1 + 24 * num_observations / (1. - correlation ** 2)) ** .5) ** .5)
    return int(bins)

def calculate_mutual_information(
    x: np.ndarray,
    y: np.ndarray,
    norm: bool = False
) -> float:
    num_bins = calculate_number_of_bins(x.shape[0], correlation=np.corrcoef(x, y)[0, 1])
    histogram_xy = np.histogram2d(x, y, num_bins)[0]
    mutual_information = mutual_info_score(None, None, contingency=histogram_xy)

    if norm:
        marginal_x = ss.entropy(np.histogram(x, num_bins)[0])
        marginal_y = ss.entropy(np.histogram(y, num_bins)[0])
        mutual_information /= min(marginal_x, marginal_y)

    return mutual_information

Variation of Information: A Simplified Guide

Understanding Variation of Information

Variation of Information (VI) measures how much one variable tells us about another. It has two terms:

• Uncertainty in $X$ given $Y$: $H[X|Y]$
• Uncertainty in $Y$ given $X$: $H[Y|X]$

So, the formula becomes:

We can also express it using other measures like Mutual Information ($I$) and joint entropy ($H[X, Y]$):

or

Normalized VI

To compare VI across varying population sizes, we can normalize it:

An alternative normalized metric is:

Calculating Basic Measures: Entropy and Mutual Information

These functionalities are available in both Python and Julia in the RiskLabAI library.

Continuous Variables and Discretization

For continuous variables, the entropy is calculated using integration. But in practice, we discretize the continuous data into bins to approximate entropy. For a Gaussian variable:

The entropy can be estimated as:

For optimal binning, we can use formulas derived by Hacine-Gharbi and others. These vary depending on whether you are looking at the marginal entropy or the joint entropy.

Calculating Variation of Information with Optimal Binning

import numpy as np
import scipy.stats as ss
from sklearn.metrics import mutual_info_score

def calculate_number_of_bins(
    num_observations: int,
    correlation: float = None
) -> int:
    if correlation is None:
        z = (8 + 324 * num_observations + 12 * (36 * num_observations + 729 * num_observations ** 2) ** .5) ** (1 / 3.)
        bins = round(z / 6. + 2. / (3 * z) + 1. / 3)
    else:
        bins = round(2 ** -.5 * (1 + (1 + 24 * num_observations / (1. - correlation ** 2)) ** .5) ** .5)
    return int(bins)

def calculate_variation_of_information_extended(
    x: np.ndarray,
    y: np.ndarray,
    norm: bool = False
) -> float:
    num_bins = calculate_number_of_bins(x.shape[0], correlation=np.corrcoef(x, y)[0, 1])
    histogram_xy = np.histogram2d(x, y, num_bins)[0]
    mutual_information = mutual_info_score(None, None, contingency=histogram_xy)
    marginal_x = ss.entropy(np.histogram(x, num_bins)[0])
    marginal_y = ss.entropy(np.histogram(y, num_bins)[0])
    variation_xy = marginal_x + marginal_y - 2 * mutual_information

    if norm:
        joint_xy = marginal_x + marginal_y - mutual_information
        variation_xy /= joint_xy

    return variation_xy

The code above shows how to calculate the Variation of Information with optimal binning in both Python and Julia. If you set norm=True, you'll get the normalized value.

Understanding Partitions in Data Sets

A partition, denoted as $P$, is a way to divide a dataset, $D$, into non-overlapping subsets. Mathematically, these subsets $D_k$ follow three main properties:

• Every subset contains at least one element, i.e., $\|D_k\| > 0$.
• Subsets do not overlap, i.e., $D_k \cap D_l = \varnothing$, for $k \neq l$.
• Together, the subsets cover the entire dataset, i.e., $\bigcup_{k=1}^{K} D_k = D$.

Metrics for Comparing Partitions

We define the uncertainty or randomness associated with a partition $P$ in terms of entropy, given by:

Here, $p[k]$ is the probability of a randomly chosen element from $D$ belonging to the subset $D_k$.

If we have another partition $P'$, we can define several metrics like joint entropy, conditional entropy, mutual information, and variation of information to compare the two partitions. These metrics provide a way to measure the similarity or dissimilarity between two different divisions of the same dataset.

Applications in Machine Learning

Variation of information is particularly useful in unsupervised learning to compare the output from clustering algorithms. It offers a normalized way to compare partitioning methods across various datasets.

Experimental Results Summarized

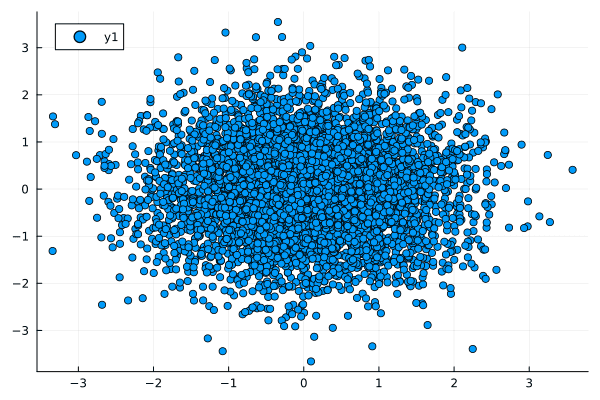
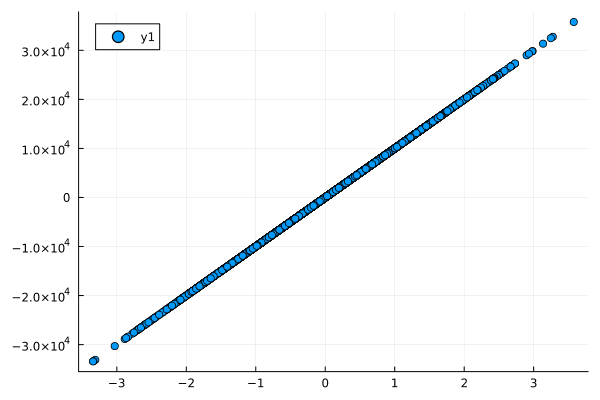
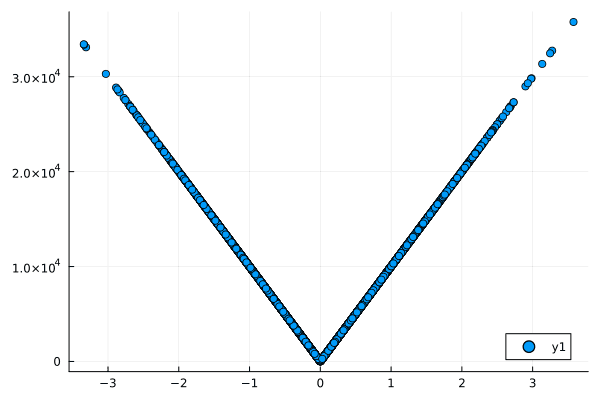
• No Relationship: When there's no relation between two variables, both correlation and normalized mutual information are close to zero.
• Linear Relationship: For a strong linear relationship, both metrics are high but the mutual information is slightly less than 1 due to some uncertainty.
• Nonlinear Relationship: In this case, correlation fails to capture the relationship, but normalized mutual information reveals a substantial amount of shared information between the variables.

Figures:

References

1. De Prado, M. L. (2018). Advances in financial machine learning. John Wiley & Sons.
2. De Prado, M. M. L. (2020). Machine learning for asset managers. Cambridge University Press.