Table of Contents

The Tone, the Signal and the Noise

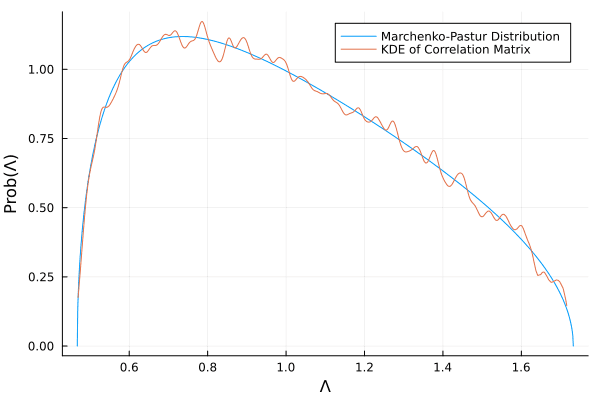
Here's how the Marcenko-Pastur PDF is mathematically defined:

f[\lambda]= \begin{cases}\frac{T}{N} \frac{\sqrt{\left(\lambda_{+}-\lambda\right)\left(\lambda-\lambda_{-}\right)}}{2 \pi \lambda \sigma^{2}} & \text{if } \lambda \in\left[\lambda_{-}, \lambda_{+}\right] \\ 0 & \text{if } \lambda \notin\left[\lambda_{-}, \lambda_{+}\right]\end{cases}

You can fit this distribution to your eigenvalues to separate the signal from the noise. Once the noise has been identified, it is possible to denoise the covariance matrix, thereby improving the reliability of any subsequent analyses.

Below are code snippets for the discussed methodologies, available in both Python and Julia in the RiskLabAI library.

Python Julia

Python	Julia
`def marcenkoPasturPDF(var, q, pts): def PCA(matrix): def fitKDE(obs, bwidth, kernel, x):`	`function pdfMarcenkoPastur(var, ratio, points) function PCA(matrix) function KDE(observations; bandWidth, kernel, valuesForEvaluating)`

def marcenkoPasturPDF(var, q, pts):

def PCA(matrix):

def fitKDE(obs, bwidth, kernel, x):

function pdfMarcenkoPastur(var, ratio, points)

function PCA(matrix)

function KDE(observations; bandWidth, kernel, valuesForEvaluating)

View More: Python | Julia

We also discussed the limitations of commonly used methods like shrinkage for conditioning covariance matrices and presented an alternative approach for denoising.

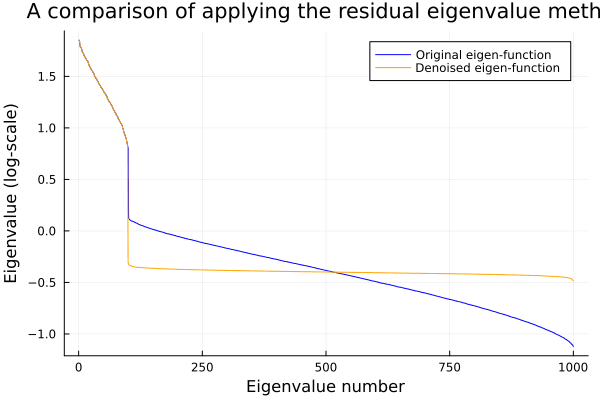
The denoising methodology aims to preserve the signal while removing the noise. It first identifies the eigenvalues associated with noise and then adjusts them to enhance the signal-to-noise ratio.

Python	Julia
`def denoisedCorr(eval, evec, nfacts):`	`function denoisedCorr(eigenValues, eigenVectors, numberFactors)`

View More: Python | Julia

Detoning: Simplifying the Math

Detoning is a technique used to remove the market influence from a financial correlation matrix. This is particularly useful in clustering algorithms that aim to identify relationships between specific financial assets. Removing the market influence makes it easier for these algorithms to group assets based on their individual characteristics rather than the broader market trends.

The detoned correlation matrix is given by:

\tilde{C}_2 = C_1 - W_M \Lambda_M W_M^\prime

Here, we adjust the correlation matrix (C_1) by subtracting (W_M \Lambda_M W_M^\prime), where (W_M) and (\Lambda_M) are the eigenvectors and eigenvalues associated with the market.

For those interested in portfolio optimization, the optimal allocations in the original asset basis can be computed as:

\omega^{*} = W_{+} f^{*}

Python	Julia
`def detoneCorrMatrix(C1: np.ndarray) -> np.ndarray:`	`function detoneCorrMatrix(C1::Array{Float64})::Array{Float64}`

View More: Python | Julia

Experimental Results: A Summary

Minimizing Portfolio Variance

Experiments show that using denoised and detoned covariance matrices can help in constructing better portfolios. Specifically, these treated matrices offer benefits when we try to minimize the portfolio variance.

Python	Julia
`def minVariancePortfolio(cov: np.ndarray) -> np.ndarray:`	`function minVariancePortfolio(cov::Array{Float64})::Array{Float64}`

View More: Python | Julia

Maximizing Sharpe Ratio

Similar experiments aimed at maximizing the Sharpe ratio of a portfolio also showed remarkable improvements when using denoised and detoned matrices.

Python	Julia
`def maxSharpeRatioPortfolio(cov: np.ndarray, mu: np.ndarray) -> np.ndarray:`	`function maxSharpeRatioPortfolio(cov::Array{Float64}, mu::Array{Float64})::Array{Float64}`

View More: Python | Julia

References

De Prado, M. L. (2018). Advances in financial machine learning. John Wiley & Sons.
De Prado, M. M. L. (2020). Machine learning for asset managers. Cambridge University Press.