The Need For Structure

Many people use Time bars to make sense of financial market data, but they're not the best choice. Why? First, trading isn't consistent throughout the day. Second, different types of bars can help solve this issue, like bars based on trading activity. For example, the function timeBar uses two things: a dataset of raw financial data (tickData) and how often you want the data to be updated (frequency). The function then gives you a new dataset that's easier to look at.

def timeBar(
tickData,
frequency
):

function timeBar(
tickData,
frequency
)

View More: Python | Julia

You can also use Tick bars. This method collects specific variables (like timestamp, VWAP, opening price, etc.) every time a set number of trades happen. For example, you get new data every 1,000 trades. This is more in sync with the rate at which new info comes into the market.

def tickBar(
tickData,
tickPerBar = 10,
numberBars = None
):

function tickBar(
tickData,
tickPerBar = 10,
numberBars = nothing
)

View More: Python | Julia

But, Tick bars have a downside. Sometimes, one trade can look like many smaller trades due to how trading systems work. This can mess up your count.

You can also use Volume bars. They update every time a certain amount of trading volume occurs.

def volumeBar(
tickData,
volumePerBar = 10000,
numberBars = None
):

function volumeBar(
tickData,
volumePerBar = 10000,
numberBars = nothing
)

View More: Python | Julia

Dollar bars are another option. They update every time a fixed amount of money is traded in the market. This is helpful when you're looking at big price changes over time.

Let's say you're watching a stock that doubled its price. To sell some of that stock later, you'd need half as many shares as you bought initially. This method keeps things proportional and makes it easier to analyze big price moves.

The number of Dollar bars remains pretty consistent, unlike Tick and Volume bars that can vary a lot. Below are some graphs that show the number of bars per day for these different methods.

def dollarBar(
tickData,
dollarPerBar = 100000,
numberBars = None
):

function dollarBar(
tickData,
dollarPerBar = 100000,
numberBars = nothing
)

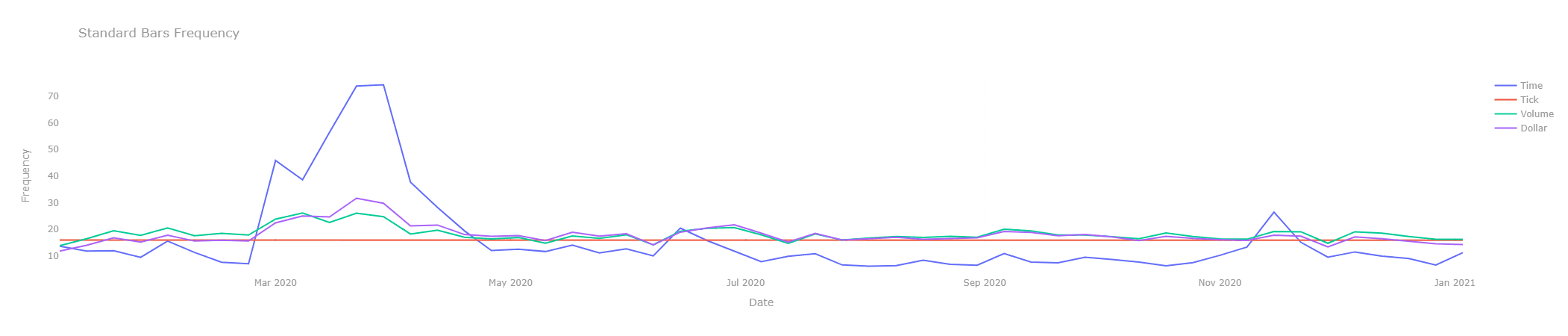
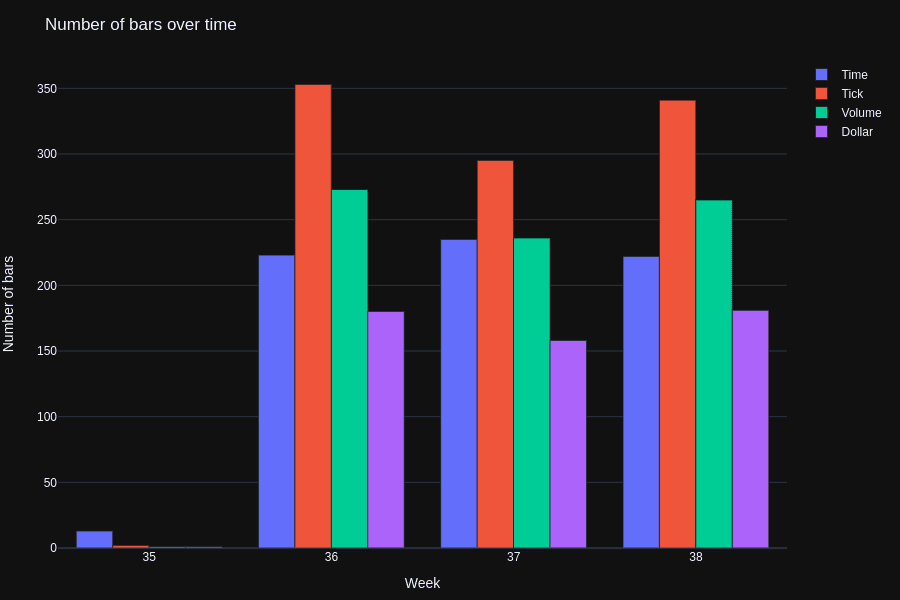
View More: Python | Julia

Information-driven Bars

Understanding Imbalance Bars in Financial Time Series Analysis with RiskLab

Financial time series data, like stock prices or volumes, can be very noisy and challenging to analyze directly. Imbalance bars offer a way to cope with such issues by forming "bars" or samples based on imbalances in the tick, volume, or dollar value of the traded assets. This blog post explains how to implement and understand Tick Imbalance Bars (TIBs), Volume Imbalance Bars (VIBs), and Dollar Imbalance Bars (DIBs) in both Python and Julia using the RiskLabAI library.

This post is aimed at making the concept clear to university-level international students, so it will be simple yet informative.

Tick Imbalance Bars (TIBs)

Consider a sequence of ticks $(p_t, v_t)$ where $p_t$ is the price at tick $t$ and $v_t$ is the volume at tick $t$. To form Tick Imbalance Bars (TIBs), we use a tick rule defined by $b_t$:

Here, $b_t$ can be either -1 or 1, and it essentially captures whether the tick was an up-tick or a down-tick compared to the previous tick.

Steps for Implementing TIBs

1. Tick Imbalance Calculation:

2. Predicted Tick Imbalance:

3. Bar Formation Rule:

Before the code snippet, we'd like to inform you that these functionalities are available in both Python and Julia through the RiskLabAI library.

def infoBar(tickData,
type = "volume",
tickExpectedInit = 2000):

function infoBar(tickData,
type::String = "volume",
tickExpectedInit = 2000)

View More: Python | Julia

Volume and Dollar Imbalance Bars (VIBs and DIBs)

We can extend the concept of TIBs to form Volume Imbalance Bars (VIBs) and Dollar Imbalance Bars (DIBs) using the same tick rule $b_t$.

Steps for Implementing VIBs and DIBs

1. Imbalance Calculation:

2. Predicted Imbalance:

We define $v^+$ and $v^-$ as the components contributed by buys and sells respectively. Thus,

3. Bar Formation Rule:

Before the code snippet, we'd like to inform you that these functionalities are available in both Python and Julia through the RiskLabAI library.

def infoBar(tickData,
type = "volume",
tickExpectedInit = 2000):

function infoBar(tickData,
type::String = "volume",
tickExpectedInit = 2000)

View More: Python | Julia

Imbalance bars help to capture the underlying imbalances in tick, volume, and dollar values of trades. This can be crucial for extracting meaningful patterns and making informed trading decisions. Feel free to explore these concepts further using the RiskLabAI library.

Order Flow Imbalance

Order flow imbalance is a crucial indicator in financial markets, often used to monitor and anticipate market movements. It is typically measured by analyzing the sequence of buy and sell orders in terms of ticks, volumes, and dollar values. Monitoring these sequences can offer valuable insights, especially when they deviate from our expectations. In this blog post, we'll delve into how to quantitatively define and measure order flow imbalances using algorithms implemented in RiskLab's library, available in both Python and Julia.

Definitions and Theoretical Background

Ticks, Volumes, and Dollar Values

Ticks are the smallest price movements that an asset can make, either upwards or downwards. Volumes indicate the number of assets being traded, and the dollar value represents the financial size of the trade.

Calculating the Current Run's Length

The term "run" refers to a consecutive sequence of buys or sells in the market. We define the length of a current run, $\theta_T$, using the following equation:

Here, $b_t$ is either 1 for a buy or -1 for a sell at time $t$, and $T$ is the length of the sequence.

Predicting the Value of $\theta_T$

To set our expectations, we also need to predict $\theta_T$ at the start of a time bar. We use $E_0$ to denote expectations based on available information at time $t=0$.

In practice, both $E_0[T]$ and $P[b_t=1]$ can be estimated using exponentially weighted moving averages from past data.

Tick Runs Bar (TRB)

A Tick Runs Bar (TRB) is a subset of ticks $T^*$ that satisfies the following condition:

Volume and Dollar Runs Bars (VRBs and DRBs)

Volume Runs Bars (VRBs) and Dollar Runs Bars (DRBs) extend the notion of runs to volumes and dollars traded, respectively.

1. Volume Runs Bars (VRBs)

2. Dollar Runs Bars (DRBs)

In this context, $v_t$ can represent either the volume or the dollar value.

We also need to calculate the predicted $\theta_T$ as:

And finally, define the VRB with $T^*$:

Implementing the Algorithms with RiskLab

def calculate_theta_T(
T: int,
sequence: List[int]
) -> int:

function calculate_theta_T(
T::Int,
sequence::Array{Int, 1}
)::Int

These functionalities are available in both Python and Julia in the RiskLab library.

By employing these algorithms, we can effectively monitor the order flow imbalances and adjust our trading strategies accordingly.

Understanding order flow imbalance is crucial for making informed decisions in financial markets. With RiskLab's Python and Julia libraries, implementing these complex algorithms becomes a straightforward task, empowering traders and researchers alike.

Feel free to check out our GitHub repositories for Python and Julia to explore these functionalities in more depth.

References

1. De Prado, M. L. (2018). Advances in financial machine learning. John Wiley & Sons.
2. De Prado, M. M. L. (2020). Machine learning for asset managers. Cambridge University Press.