Financial Data Weighting

The Challenge of Non-IID Data in Finance

You might have noticed that many financial models rely on the assumption that data points are independent and identically distributed (IID). However, this is often not the case in real-world financial applications. This blog post will show you how to leverage sample weights to address these challenges.

When and Why Does the IID Assumption Fail?

Financial labels, such as returns, are often based on overlapping time intervals. This overlapping nature makes these labels non-IID. While some machine learning applications can manage without the IID assumption, most financial models struggle without it. Let's explore some techniques to mitigate this issue.

Defining Concurrency in Financial Labels

We say that two labels, $y_i$ and $y_j$, are concurrent if they depend on the same return. To quantify this, we use an indicator function, $\mathbb{I}_{t, i}$, defined as:

The number of labels that are concurrent at time $t$ is represented by $c_t = \sum_{i=1}^{I} \mathbb{I}_{t, i}$.

def optimal_trading_rule(
sigma: float,
phi: float
) -> Tuple[float, float]:

function optimal_trading_rule(
sigma::Float64,
phi::Float64
) -> Tuple{Float64, Float64}

View More: Python | Julia

Measuring Label Uniqueness

Next, we introduce a function to measure label uniqueness at a given time $t$. This function, denoted as $u_{t, i}$, is defined as:

The average uniqueness of a label $i$ over time $T$ is given by:

In both RiskLabAI's Python and Julia libraries, you can estimate label uniqueness using specific functions.

def mpSampleWeight(
timestamp: pd.DataFrame,
concurrencyEvents: pd.DataFrame,
molecule: pd.Series
) -> None:

function sampleWeight(
timestamp::DataFrame,
concurrencyEvents::DataFrame,
molecule::Vector
)::DataFrame

View More: Python | Julia

Overlapping Outcomes Problem in Bootstrapping

When using bootstrapping to sample $I$ items from a set of $I$ items with replacements, there's a chance some items get selected more than once, leading to overlapping outcomes. For larger sets, the probability of not selecting a particular element converges to $e^{-1}$. As a result, only about $2/3$ of the observations are unique, making bootstrapping inefficient.

Solving with Sequential Bootstrapping

Sequential bootstrapping assigns different probabilities to observations, making the sampling process more efficient. The probability density for selecting observation $i$ at step $m$ is calculated using:

where $\bar{u}_{i}^{(m)}$ and $u_{t, i}^{(m)}$ are computed using specific formulas. This approach minimizes the chance of selecting overlapping outcomes.

Index Matrix Calculation

Both Python and Julia libraries in RiskLabAI offer functions to calculate the index matrix. In Python, it's index_matrix and in Julia, it's indexMatrix.

def index_matrix(
barIndex: pd.DataFrame,
timestamp: pd.DataFrame
) -> np.array:

function indexMatrix(
barIndex::Vector,
timestamp::DataFrame
)::Matrix

View More: Python | Julia

Calculating Average Uniqueness

Both libraries also offer functions to calculate the average uniqueness of the samples. In Python, it's averageUniqueness and in Julia, it's also averageUniqueness.

def averageUniqueness(
indexMatrix: np.array
) -> np.array:

function averageUniqueness(
IndexMatrix::Matrix
)::Vector

View More: Python | Julia

Sequential Bootstrap Sampling

Finally, for sequential bootstrap sampling, the Python function is SequentialBootstrap and in Julia, it's sequentialBootstrap.

def sequential_bootstrap(
indexMatrix: np.array,
sampleLength: int
) -> np.array:

function sequentialBootstrap(
indexMatrix::Matrix,
sampleLength::Int64
)::Vector

View More: Python | Julia

These functionalities are available in both Python and Julia in the RiskLabAI library. For more details, you can visit the GitHub repositories for each language.

Monte Carlo Verification of Method Effectiveness

Our goal is to assess the performance of different bootstrapping techniques. We focus on comparing the Sequential Bootstrap method with the Standard Bootstrap. We accomplish this through Monte Carlo experiments that utilize random timestamps and various other parameters.

Generating Random Timestamps

We generate random timestamps for each observation within the given parameters. The function randomTimestamp does this job in both the Python and Julia libraries of RiskLabAI.

def randomTimestamp(
nObservation: int,
nBars: int,
maximumHolding: int
) -> None:

function randomTimestamp(
nObservation::Int64,
nBars::Int64,
maximumHolding::Int64
)::DataFrame
end

View More: Python | Julia

Monte Carlo Simulation for Sequential Bootstraps

We run Monte Carlo simulations to compare the Sequential Bootstrap with the Standard Bootstrap using the monteCarloSimulationforSequentionalBootstraps function.

def MonteCarloSimulationforSequentionalBootstraps(
nObservation: int,
nBars: int,
maximumHolding: int
) -> None:

function monteCarloSimulationforSequentionalBootstraps(
nObservation::Int64,
nBars::Int64,
maximumHolding::Int64
)::Tuple{Float64,Float64}
end

View More: Python | Julia

Multiple Iterations

For a more robust assessment, we run the Monte Carlo simulation in multiple iterations for both Sequential and Standard Bootstraps using SimulateSequentionalVsStandardBootstrap.

def SimulateSequentionalVsStandardBootstrap(
iteration: int,
nObservation: int,
nBars: int,
maximumHolding: int
) -> None:

function SimulateSequentionalVsStandardBootstrap(
iteration::Int64,
nObservation::Int64,
nBars::Int64,
maximumHolding::Int64
)::Tuple{Vector,Vector}
end

View More: Python | Julia

Results and Figures

The Monte Carlo tests reveal differences between Standard and Sequential Bootstraps.

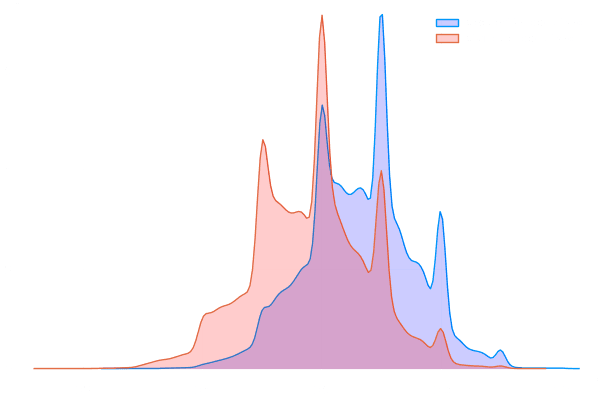
We also examine the histogram of the average uniqueness for both bootstrapping techniques. This gives us insights into how unique each sample is, allowing for better analysis.

Weighting Returns in Machine Learning Models

In machine learning for finance, it's critical to weigh data properly. Returns with high absolute values should have more weight than those with low absolute returns. The uniqueness of an observation also plays a role in determining its weight.

Calculating Sample Weight with Return Attribution

In RiskLabAI, we offer functions to handle this weight assignment. The Julia function sampleWeight and the Python function mpSampleWeightAbsoluteReturn both serve this purpose.

def mpSampleWeightAbsoluteReturn(
timestamp :pd.DataFrame,
concurrencyEvents :pd.DataFrame,
returns :pd.DataFrame,
molecule :np.array
) -> None:

function sampleWeight(
timestamp :pd.DataFrame,
concurrencyEvents :pd.DataFrame,
returns :pd.Series,
molecule :np.array
)

View More: Python | Julia

These functionalities are available in both Python and Julia in the RiskLabAI library.

Time-Decay of Sample Weights

Over time, older market data becomes less relevant. Thus, a time-decay factor is applied to the sample weights. The decay factor is defined by a user-specified parameter $c$. The weight decay follows the formula:

where $a$ and $b$ are calculated based on boundary conditions and $c$.

Again, RiskLabAI has built-in functions for this. The Julia function TimeDecay and its Python equivalent handle weight adjustments based on time.

def timeDecay(
weight :pd.Series,
clfLastW = 1.0 :float
) -> None:

function TimeDecay(
weight;
clfLastW = 1.0
)::Nothing

View More: Python | Julia

These functionalities are available in both Python and Julia in the RiskLabAI library.

Cases to Consider for Time-Decay

• $c=1$ implies no decay.
• $0 < c < 1$ implies linear decay, with all observations still getting some weight.
• $c=0$ leads to weights converging to zero as they age.
• $c < 0$ implies that the oldest observations get zero weight.

References

1. De Prado, M. L. (2018). Advances in financial machine learning. John Wiley & Sons.
2. De Prado, M. M. L. (2020). Machine learning for asset managers. Cambridge University Press.